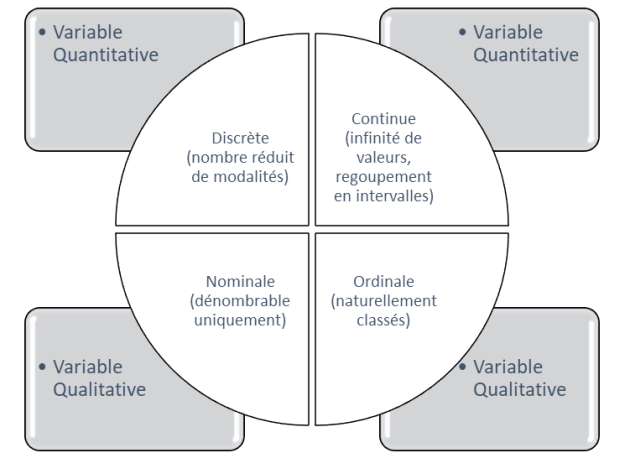
Typologie des variables et représentations graphiques associées
Nous avons donc dans un premier temps énuméré 10 représentations graphiques courantes de séries statistiques et quelques variantes pour certaines représentations. Nous savons également que les variables d'une série statistique peuvent être classées par typologie.
Rappel :
Il est donc indispensable de mettre en relation ces deux éléments afin de révéler les compatibilités, incompatibilités et inutilités.
Variables Qualitatives
Fondamental :
Pour les variables qualitatives, il convient de distinguer leurs caractères nominal ou ordinal.
Variables qualitatives nominales
Fondamental :
Ces variables peuvent être dénombrées pour ensuite être représentées dans un graphique approprié. Nous aurons donc une répartition des individus en fonction des modalités renseignées : nombre de femmes et d'hommes de la population, nombre d'individus par origine géographique, etc.
Bien entendu la valorisation de ces modalités peut être relativisée, donc calculée en pourcentage de la population totale pour être représentée. Le contexte de l'étude statistique peut également amener à utiliser des représentations qui ne semblent pas appropriées de prime abord.
Méthode :
En fonction des caractères des variables qualitatives nominales, nous pouvons en déduire la synthèse suivante sur les représentations graphiques compatibles :
Exemple : Liste de touristes recensés pour une location
Touristes | Origine |
|---|---|
Individu 1 | Europe de l'Ouest |
Individu 2 | Asie |
Individu 3 | Amérique du Nord |
Individu 4 | Asie |
Individu 5 | Asie |
Individu 6 | Europe de l'Ouest |
Individu 7 | Europe centrale |
Individu 8 | Europe centrale |
Individu 9 | Europe de l'Ouest |
Individu 10 | Amérique du nord |
Individu 11 | Asie |
Individu 12 | Europe de l'Ouest |
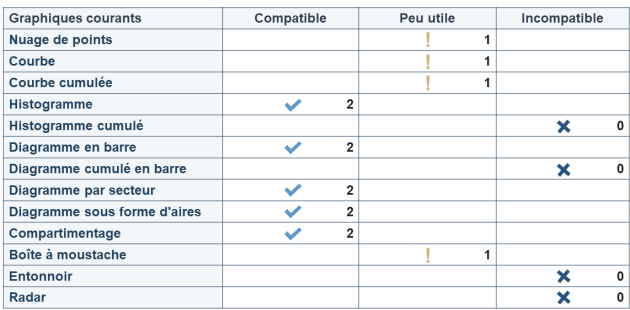
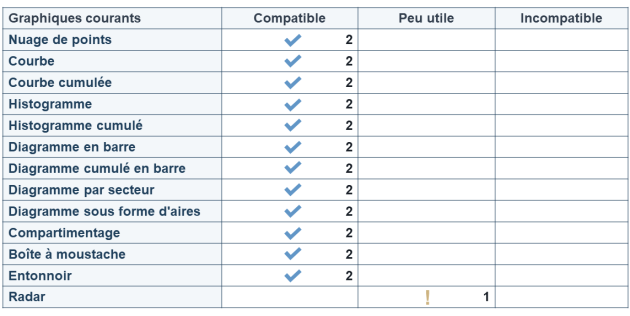
Nous avons donc une variable qualitative nominale avec 4 modalités, nous pouvons regrouper par modalité les individus et ainsi obtenir les représentations graphiques compatibles :
Variables qualitatives ordinales
Fondamental :
Ces variables classées peuvent être dénombrées et cumulées pour ensuite être représentées dans un graphique approprié. Nous aurons donc une répartition des individus en fonction des modalités renseignées : nombre de clients satisfaits, insatisfaits, degré de compétences, etc.
Bien entendu la valorisation de ces modalités peut être relativisée, donc calculée en pourcentage de la population totale pour être représentée. Le contexte de l'étude statistique peut également amener à utiliser des représentations qui ne semblent pas appropriées de prime abord.
Méthode :
En fonction des caractères des variables qualitatives ordinales, nous pouvons en déduire la synthèse suivante sur les représentations graphiques compatibles :
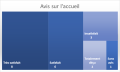
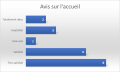
Exemple : Résultats d'une enquête de satisfaction sur la qualité d'accueil d'un hébergement de tourisme
Critère | Nombre de réponses |
|---|---|
Très satisfait | 8 |
Satisfait | 6 |
Sans avis | 1 |
Insatisfait | 3 |
Totalement déçu | 2 |
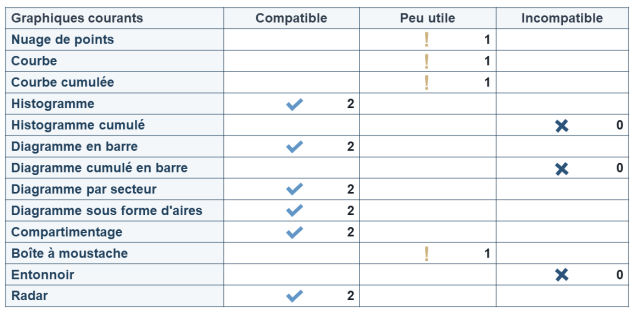
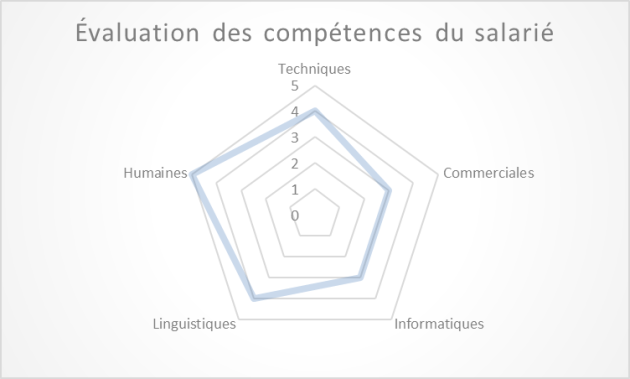
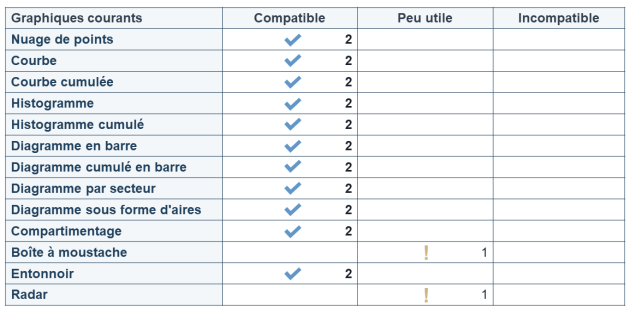
Nous avons donc une variable qualitative ordinale avec 5 modalités, nous pouvons obtenir les représentations graphiques compatibles :
Exemple :
Dans la première partie, nous avons réalisé un diagramme sous forme radar qui correspond à cette catégorie de variable :
Variables Quantitatives
Fondamental :
Pour les variables quantitatives, il convient de distinguer leurs caractères discret ou continu.
Variables quantitatives discrètes
Fondamental :
Ces variables peuvent être dénombrées, additionnées, cumulées, faire l'objet de moyennes ou de tendances pour ensuite être représentées dans un graphique approprié. Le panel de types de graphiques utilisés sera donc large, et la pertinence sera souvent liée au contexte.
Méthode :
En fonction des caractères des variables quantitatives discrètes, nous pouvons en déduire la synthèse suivante sur les représentations graphiques compatibles :
Exemple :
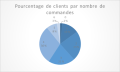
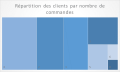
Sur une population de 120 clients, nous avons identifié le nombre de commandes que chacun a passé durant l'année. Cette série statistique nous permet de fait la synthèse suivante :
Nombre de commandes passées par an | Nombre de clients concernés |
|---|---|
0 | 2 |
1 | 16 |
2 | 28 |
3 | 25 |
4 | 36 |
5 | 10 |
6 | 3 |
Nous avons donc une variable quantitative discrète avec 7 modalités, nous pouvons obtenir les représentations graphiques compatibles :
Conseil :
Comme vous l'aurez remarqué, afin de rendre lisible et compréhensible le graphique, il est souvent nécessaire de modifier les paramètres relatifs aux légendes et à l'affichage des informations.
Variables quantitatives continues
Fondamental :
Ces variables peuvent être dénombrées, additionnées, cumulées, faire l'objet de moyennes ou de tendances pour ensuite être représentées dans un graphique approprié. Elles seront souvent regroupées en intervalles afin d'assurer une meilleure lisibilité. Le panel de types de graphiques utilisés sera donc large, et la pertinence sera souvent liée au contexte.
Méthode :
En fonction des caractères des variables quantitatives continues, nous pouvons en déduire la synthèse suivante sur les représentations graphiques compatibles :
Exemple :
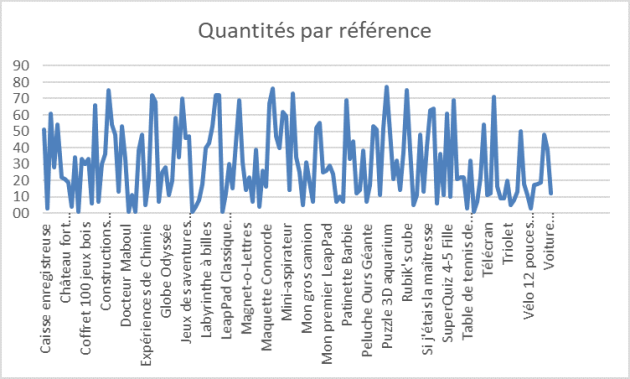
Une série statistique d'un magasin de jouets reprend 169 références vendues afin d'analyser les ventes en valeur sur une période.
Le nombre de modalités étant sensiblement identique au nombre d'individus, un graphique sous forme de courbe ou d'histogramme aura peu d'intérêt tant il sera illisible :
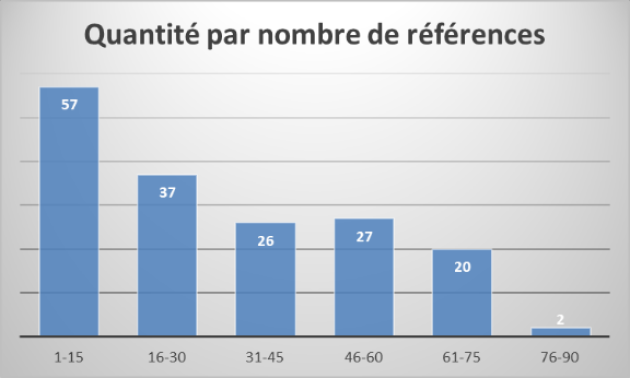
Seul un regroupement par intervalles permettra une lecture plus aisée :
Ainsi nous comprenons que 57 références ont fait l'objet de 0 à 15 ventes.
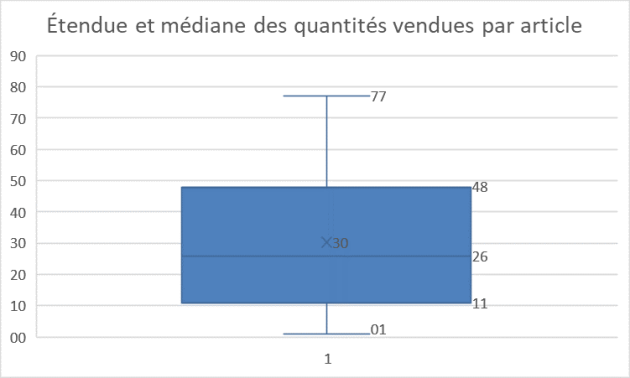
Méthode :
En utilisant les intervalles, nous pouvons donc nous appuyer sur les mêmes types de graphiques que lorsque nous traitons des variables quantitatives discrètes.
Exemple :
Selon le même exemple, pour un graphique sous forme de boîte à moustaches, nous obtiendrons :
