Comment reconnaître les charges variables des charges fixes ? [Méthode des coûts variables]

Comment reconnaître les charges variables des charges fixes ?

Principe

Il existe trois catégories de charges dans les entreprises :

Les charges variables,
Les charges fixes,
Les charges semi-variables.

Il existe deux méthodes pour définir les charges de l'entreprise :

Une méthode « empirique »
On admet a priori que certaines charges sont variables, d'autres fixes, (les autres étant donc considérées par définition comme semi-variables).
Il reste toutefois, avec cette méthode, le problème de la séparation des parties fixes et variables des charges semi-variables.
une méthode plus « scientifique »
Cette méthode se base sur les statistiques.
Elle est surtout utilisée pour séparer la partie variable de la partie fixe des charges semi-variables.

Méthode empirique de séparation des charges de l'entreprise

Charges variables

On range par exemple (sans calculs particuliers) dans les charges variables :

Les achats de matières ou de marchandises,
Les commissions variables des commerciaux,
La consommation d'énergie.

Autrement dit les charges variables varient proportionnellement à l'activité.

Charges fixes

On range par exemple (sans calculs particuliers) dans les charges fixes :

Les amortissements des immobilisations,
Les taxes non basées sur le chiffre d'affaires (taxe foncière, taxe sur les véhicules de sociétés, etc.),
La masse salariale mensualisée,
Le loyer.

Autrement dit les charges fixes ne varient pas en fonction de l'activité.

Attention :

Cela ne veut pas dire que les charges fixes ne « varient » jamais mais, si elles varient, ce n'est pas proportionnellement à l'activité → Elles varient par palier !

Exemple :

Le loyer d'une entreprise peut augmenter d'une période à l'autre mais il n'augmente pas en fonction du chiffre d'affaires ou des quantités vendues ou achetées !

Charges semi-variables

On peut donc considérer qu'à priori les charges semi-variables sont les autres charges !

Étude à posteriori des charges semi-variables

Exemple 1

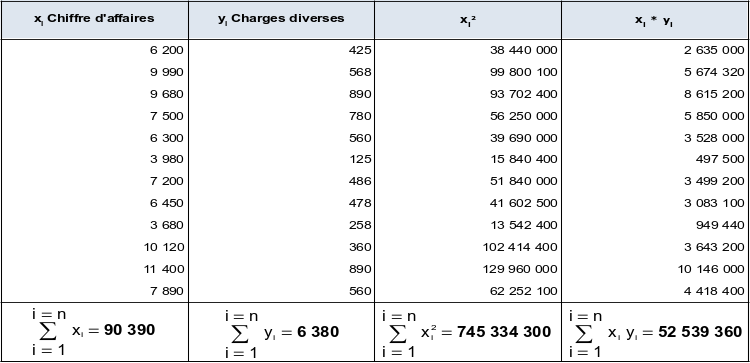
On dispose, pour l'année N de l'extrait suivant (en millions d'€) concernant des charges diverses (yi) et du chiffre d'affaires (x_i).

Mois	Chiffre d'affaires x_i (Millions d'€)	Charges diverses y_i (Millions d'€)
Janvier	6 200	425
Février	9 990	568
Mars	9 680	890
Avril	7 500	780
Mai	6 300	560
Juin	3 980	125
Juillet	7 200	486
Août	6 450	478
Septembre	3 680	258
Octobre	10 120	360
Novembre	11 400	890
Décembre	7 890	560

On s'aperçoit d'après le tableau que les charges diverses ne sont ni fixes ni variables à 100 %.

Si elles étaient fixes à 100 %, en février par exemple, les charges diverses seraient aussi de 425.

Si elles étaient variables à 100 %, en février elles auraient dû être de : \frac{425}{6 200} * 9 990 = 684,80

Conséquence

Comme ce n'est pas le cas, il s'agit donc de charges semi-variables.

Il faut donc séparer la partie variable de la partie fixe de ces charges semi-variables.

En admettant que, dans cet exemple, le nuage de points soit suffisamment allongé, on peut utiliser la méthode dite des moindres carrés.

Cette méthode consiste à remplacer (d'ajuster) la série par une droite de la forme : y = ax + b

Avec :

a = Charges variables unitaires
x = Activité (dans notre exemple → x correspondrait au chiffre d'affaires)
b = Charges fixes totales

Rappel :

a = \frac{Cov (xy)}{V (x)}

Covariance de (x,y) = Cov(xy) = Moyenne des produits - Produit des moyennes

Rappel :

Cov (xy) = [\frac{1}{N} \begin{matrix} i = n \\ \sum \\ i = 1 \end{matrix} x_{i} y_{i}] - (\bar{x} \bar{y}) avec N = Nombre d'observations

Variance de x = V(x) = Moyenne des carrés - Carré de la moyenne

Rappel :

V (x) = [\frac{1}{N} \begin{matrix} i = n \\ \sum \\ i = 1 \end{matrix} x_{i}^{2}] - {(\bar{x})}^{2} avec N = Nombre d'observations

Rappel :

\begin{matrix} Moyenne de x = \bar{x} = \frac{1}{N} \sum_{i = 1}^{1 = N} x_{i} \\ Moyenne de y = \bar{y} = \frac{1}{N} \sum_{i = 1}^{1 = N} y_{i} \\ b = \bar{y} - a \bar{x} \end{matrix}

Correction

Conséquence

En utilisant les formules et sachant qu'ici le nombre d'observations « N » = 12 → il vient :

\begin{matrix} \bar{x} = \frac{1}{N} \sum_{i = 1}^{1 = N} x_{i} = \frac{1}{12} * 90 390 = 7 532,50 \\ \bar{y} = \frac{1}{N} \sum_{i = 1}^{1 = N} y_{i} = \frac{1}{12} * 6 380 = 531,67 \end{matrix}

V (x) = [\frac{1}{N} \sum x_{i}^{2}] - {(\bar{x})}^{2} = (\frac{1}{12} * 745 334 300) - 7 {532,50}^{2} = 5 372 634,42

Cov (xy) = [\frac{1}{N} \begin{matrix} i = n \\ \sum \\ i = 1 \end{matrix} x_{i} y_{i}] - (\bar{x} \bar{y}) = (\frac{1}{12} * 52 539 360) - (7 532,50 * 531,67) = 373 475,73

a = \frac{Cov (xy)}{V (x)} = \frac{373 475,73}{5 372 634,42} = 0,0695 = 6,95 %

b = \bar{y} - (a * \bar{x}) = 531,67 - (0,0695 * 7 532,50) = 8,16

Conclusion

Avec cette méthode, la partie variable est donc égale à 6,95 % du chiffre d'affaires, et la partie fixe à 8,16 millions d'€ par mois → Soit : 8,16 x 12 = 97,92 millions d'€ pour l'exercice.

D'où la décomposition :

Partie fixe

Partie variable

90 390 * 0,0695

97,92

6 282,11

6 380,03

Remarque :

La légère différence (6 380,03 contre 6 380) vient des arrondis sur la valeur de « a ».