Seuil de Rentabilité (SR) [Méthode des coûts variables]

Principe du raisonnement

Le seuil de rentabilité représente le chiffre d'affaires minimum qu'une entreprise doit réaliser pour, qu'à ce niveau de chiffre d'affaires, il n'y ait pas de bénéfice, ni de perte.

Autrement dit :

SR = Chiffre d'affaires pour que le résultat (correspondant à ce chiffre d'affaires) = 0

Donc on peut écrire :

Chiffre d'affaires

- Coût de revient variable

= Marge sur coût variable (M/CV)

- Charges Fixes d'Exploitation(CFD et CFI)

= 0

Le seuil de rentabilité est donc atteint lorsque la marge sur coût variable est égale aux charges fixes d'exploitation.

Calcul du seuil de rentabilité en €

La question à se poser

Combien doit-on faire de chiffre d'affaires pour que la M/CV dégagée, par ce chiffre d'affaires, soit égale aux charges fixes d'exploitation ?

Exemple

	Total	%
Chiffre d'affaires - Charges variables totales	3 200 000 - 1 920 000	100 % 60 %
= Marge sur coût variable (M/CV)	1 280 000	40 %
- Charges fixes d'exploitation	- 800 000	-
= Résultat	480 000	15,00 %

1ère approche possible pour calculer le SR

Quand le chiffre d'affaires total est de 3 200 000 €, la M/CV totale est de 1 280 000 €. Combien doit-on faire de chiffre d'affaires pour que la M/CV soit égale à 800 000 € (montant des charges fixes d'exploitation).

Il suffit de poser l'expression suivante :

CA	M/CV
3 200 000 x	1 280 000 800 000

CA

M/CV

3 200 000

x

1 280 000

800 000

Conséquence

En utilisant le « produit en croix », il vient → (3 200 000 * 800 000) = (x * 1 280 000)

\to x = \frac{3 200 000 * 800 000}{1 280 000} \to x = 2 000 000

Autrement dit, que venons-nous d’écrire ? \to SR en € = \frac{Chiffre d'affaires total * Charges fixes d'exploitation}{M/CV totale}

Le seuil de rentabilité est atteint lorsque le chiffre d'affaires atteint 2 000 000 €. Donc, normalement, le résultat devrait être de 0 pour un chiffre d'affaires de 2 000 000 de €.

Procédons à la vérification

Chiffre d'affaires - Coût de revient variable	2 000 000 (1) - 1 200 000
= Marge sur coût variable (M/CV)	(2) 800 000
- Charges fixes d'exploitation (CFD et CFI)	- 800 000
= Résultat	0

(1) → Les charges variables sont par définition proportionnelles au chiffre d'affaires.

→ Si pour le chiffre d'affaires total elles sont de 60 %, elles sont aussi de 60 % pour un chiffre d'affaires de

2 000 000 € → 2 000 000 * 60 % = 1 200 000.

(2) → Même remarque que pour les charges variables → Pour le chiffre d'affaires total, le % de M/CV = 40 %.

→ Pour un chiffre d'affaires de 2 000 000, la M/CV doit être aussi de 40 % → 2 000 000 * 0,40 = 800 000.

Vous pouvez constater que le résultat est bien de zéro.

Grâce à ce niveau de chiffre d'affaires (2 000 000 €), l'entreprise a réussi à couvrir l'ensemble de ses charges fixes d'exploitation et les charges variables pour atteindre ce chiffre d'affaires.

Donc, tout chiffre d'affaires supérieur à 2 000 000 € entraînera des bénéfices.

2ème approche possible pour calculer le SR

On sait, par définition :

Que les charges variables varient proportionnellement à l'activité (donc au chiffre d'affaires),
Que, par conséquent, la M/CV varie également proportionnellement au chiffre d'affaires,
Qu'au seuil de rentabilité → M/CV = Charges fixes d'exploitation.

Conséquence

Le % de M/CV sera toujours le même, quel que soit le chiffre d'affaires !

→ Le % (ou le taux) de M/CV pour le chiffre d'affaires total = % de M/CV au seuil de rentabilité.

Autrement dit \to Seuil de rentabilité en € (x) = \frac{Charges fixes d'exploitation}{% de M/CV}

Remarque :

C'est cette 2^ème approche que l'on doit privilégier, car elle s'applique très bien à la représentation graphique du seuil de rentabilité.

Reprenons le même exemple que ci-avant → CF d'exploitation = 800 000 € et % M/CV = 40 %.

\to Seuil de rentabilité en € = \frac{800 000}{0,40}

→ Seuil de rentabilité en € = 2 000 000

On retrouve bien un seuil de rentabilité égal à 2 000 000 € comme dans la 1^ère approche.

Représentation graphique du seuil de rentabilité en €

On utilise la relation suivante → Au seuil de rentabilité, la M/CV est égale aux charges fixes.

En abscisse → x = Chiffre d'affaires
En ordonnée → y₁ = Équation de la M/CV = (% de M/CV * x) = a * x
→ y₂ = Équation des charges fixes d'exploitation = b

Conséquence

À l'intersection de y₁ et y₂ → M/CV = CF.

À l'intersection d'y₁ et d'y₂, il suffit de descendre sur l'axe des « x » (donc l'abscisse) pour lire directement le chiffre d'affaires correspondant et il s'agit donc du seuil de rentabilité.

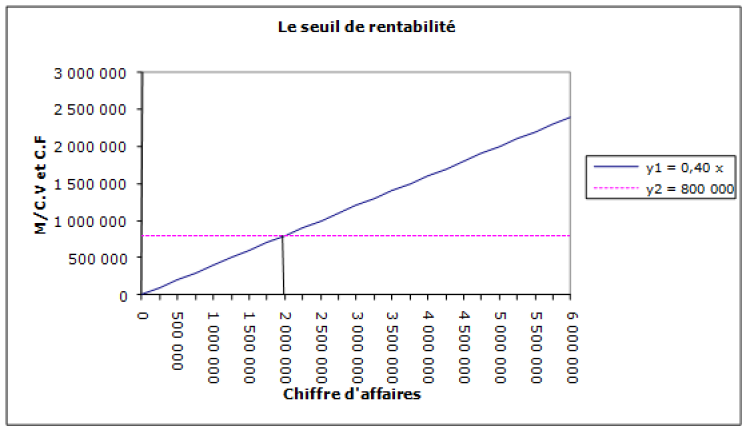
À l'intersection des deux droites, le chiffre d'affaires est égal à 2 000 000 € et donc on retrouve bien le même seuil de rentabilité qu'auparavant.

Remarque :

Jusqu'à présent, nous avons raisonné dans le cas où l'entreprise ne vendrait qu'une seule sorte de produits. Bien entendu, le raisonnement reste le même si l'entreprise vend plusieurs sortes de produits.

Mais :

M/CV totale = Somme des M/CV pour chaque type de produit.
Chiffre d'affaires total = Somme des chiffre d'affaires pour chaque type de produit.
Charges fixes d'exploitation = Rien de particulier !

Calcul du Seuil de Rentabilité en Quantité (SRQ)

Exemple

Une entreprise vend un produit P₁ → Si X₁ = Nombre de produits à vendre pour atteindre le seuil de rentabilité, on peut affirmer que le seuil de rentabilité en quantité sera atteint lorsque la M/CV sera égale aux charges fixes d'exploitation.

Donc, on peut écrire → (M/CV unitaire de P₁ * Quantité vendue de produits X₁) = CF d'exploitation.

Sachant que X₁ sera la seule inconnue, on peut écrire :

\to x_{1} = \frac{Charges fixes d'exploitation}{M/CV unitaire de p_{1}}

Reprenons l'exemple de la section 3 – A et supposons que le prix de vente du produit est de 320,00 €.

Rappel de l'énoncé

	Total	%
Chiffre d'affaires - CV totales	3 200 000 - 1 920 000	100 % 60 %
= Marge sur coût variable (M/CV)	1 280 000	40 %
- CF d'exploitation	- 800 000	-
= Résultat	480 000	15,00 %

Si le PVu est de 320,00 € → L'entreprise vend donc 10 000 articles.

Donc on peut écrire :

M/CV unitaire en € = (320,00 * 0,40) = 128,00 €

Ou

M/CV unitaire en € = 320,00 - (320,00 * 0,60) = 128,00 €

Ou

M/CV unitaire en € = 1 280 000 / 10 000 = 128,00 €

Conséquence

SRQ = 800 000 / 128,00 = 6 250 unités.

Donc, pour atteindre son SRQ, l'entreprise devra vendre 6 250 produits.

Vérification

Si SRQ = 6 250 → Alors seuil de rentabilité en € → 6 250 * 320,00 = 2 000 000 €.

On retrouve bien le même seuil de rentabilité en € que précédemment.

Remarque :

Une autre approche est possible \to SRQ = \frac{SR en €}{PVu} \to SRQ = \frac{2 000 000}{320} = 6 250 (produits)

Attention :

Dans l'hypothèse d'un SRQ qui n'est pas un chiffre entier, il faut arrondir à l'unité supérieure → Le seuil de rentabilité sera alors atteint avec certitude.

Date d'atteinte du seuil de rentabilité

Date d'atteinte si le chiffre d'affaires est régulier sur la période étudiée

La résolution (dans ce cas purement théorique) est simple mais attention aux pièges suivants !

L'entreprise ferme un mois dans l'année : dans ce cas le chiffre d'affaires est effectué sur 330 jours et non sur 360 jours.
L'exercice ne commence pas le 1^er janvier : dans ce cas bien décalé le nombre de jours par rapport au début d'exercice.

Exemple

Chiffre d'affaires annuel = 4 700 000 €.

Taux de M/CV = 28 %.

Charges fixes d'exploitation = 750 000 €.

Question

Calculer la date d'atteinte du seuil de rentabilité.

Réponse

SR en € = \frac{Charges fixes d'exploitation}{% de M/CV} = \frac{750 000}{0,28} = 2 678 571 €

Ou

\begin{matrix} SR en € = \frac{Chiffre d'affaires total * Charges fixes d'exploitation}{M/CV totale} = \frac{4 700 000 * 750 000}{4 700 000 * 0,28} \\ SR en € = 2 678 571 € \end{matrix}

Chiffre d'affaires journalier = \frac{4 700 000}{360} = 13 056 €

Remarque :

Si l'énoncé ne précise rien, on suppose que l'entreprise ne ferme pas pendant l'année.

\to SR en jours = \frac{2 678 571}{13 056} = 205,16 (jours)

\to SR en mois = \frac{205,16}{30} = 6,84 (mois)

Ce qui veut donc dire que le seuil de rentabilité est atteint 6,84 mois après le début de l'exercice !

6 mois + 0,84 mois → (6 * 30) + (0,84 * 30) = 205,20 jours,
Arrondi à 206 jours.

Conclusion

La date d'atteinte du seuil de rentabilité est le 26 juillet.

Remarque : 1

Si l'entreprise était fermée pendant le mois de juillet :

Le seuil de rentabilité total en € serait forcément identique au précédent → 2 678 572 €.
$Chiffre d'affaires journalier = \frac{4 700 000}{330} = 14 242,42$
$Seuil de rentabilité en jours = \frac{2 678 571}{14 242,42} = 188,07 jours$
Seuil de rentabilité atteint 189 jours après le 1^er janvier, sachant que l'entreprise est fermée en juillet.
- Date d'atteinte = 9 août et non 9 juillet !

Remarque : 2

En reprenant exactement le même exemple que précédemment, mais en supposant que l'exercice commence le 1^er avril.

Le seuil de rentabilité total en € serait forcément identique au précédent → 2 678 572 €.
Seuil de rentabilité atteint 189 jours après le 1er avril, sachant que l'entreprise est fermée en juillet.
- Date d'atteinte = 9 novembre !

Date d'atteinte si le chiffre d'affaires n'est pas régulier sur la période à étudier

Pour résoudre ce problème on peut utiliser le chiffre d'affaires cumulé ou bien par la M/CV cumulée.

Exemple

Vous disposez des éléments suivants concernant la répartition du chiffre d'affaires sur la période.

Mois	Chiffre d'affaires mensuel (en €)
Janvier	470 000
Février	520 000
Mars	280 000
Avril	150 000
Mai	80 000
Juin	80 000
Juillet	130 000
Août	220 000
Septembre	290 000
Octobre	620 000
Novembre	970 000
Décembre	890 000
Chiffre d'affaires annuel	4 700 000

Vous disposez par ailleurs des éléments suivants :

Taux (ou pourcentage) de M/CV = 28 %.

Charges fixes d'exploitation = 750 000 €.

1ère question - Déterminer le seuil de rentabilité en € de cette entreprise

\to SR en € = \frac{Charges fixes d'exploitation}{% de M/CV} = \frac{750 000}{0,28} = 2 678 571 €

Ou

\begin{matrix} \to SR en € = \frac{Chiffre d'affaires total * Charges fixes d'exploitation}{M/CV totale} \\ \to SR en € = \frac{4 700 000 * 750 000}{4 700 000 * 0,28} = 2 678 571 € \end{matrix}

2ème question - Déterminez la date d'atteinte du seuil de rentabilité

Problème

Le chiffre d'affaires n'est pas réparti linéairement sur l'année et donc la méthode ci-avant ne peut être appliquée ici.

Solution

Dans la question précédente nous avons trouvé le seuil de rentabilité en €, il suffit donc maintenant de trouver, grâce au chiffre d'affaires cumulé, quand il sera atteint.

Nous pouvons donc construire le tableau suivant :

Mois	Chiffre d'affaires mensuel	Chiffre d'affaires cumulé
Janvier	470 000	470 000
Février	520 000	990 000
Mars	280 000	1 270 000
Avril	150 000	1 420 000
Mai	80 000	1 500 000
Juin	80 000	1 580 000
Juillet	130 000	1 710 000
Août	220 000	1 930 000
Septembre	290 000	2 220 000
Octobre	620 000	2 840 000
Novembre	970 000	3 810 000
Décembre	890 000	4 700 000

Rappelons que le seuil de rentabilité en € = 2 678 571 € (cf calcul ci-avant).

Grâce à la série cumulée du chiffre d'affaires, on constate que le niveau de chiffre d'affaires nécessaire pour atteindre le seuil de rentabilité est atteint au cours du mois d'octobre. En effet, fin septembre le chiffre d'affaires cumulé est de 2 220 000 € → Donc fin septembre il n'est pas encore atteint !

En revanche, fin octobre le chiffre d'affaires cumulé est de 2 840 000 € → Donc le seuil de rentabilité est atteint pendant le mois d'octobre. Mais quand en octobre ?

Résolution

Dans un 1^er temps, il suffit de déterminer le chiffre d'affaires restant à réaliser, à partir de fin septembre, pour atteindre le seuil de rentabilité.

Dans un 2^ème temps, on calcule combien de jours il faudra, en octobre, pour faire ce supplément de chiffre d'affaires.

Chiffre d'affaires à réaliser pour atteindre le seuil de rentabilité durant le mois d'octobre
2 678 571 - 2 220 000 = 458 571 €
Chiffre d'affaires réalisé en octobre
2 840 000 - 2 220 000 = 620 000 € (ou donné directement par l'énoncé)
Chiffre d'affaires par jours en octobre
$\frac{620 000}{31} = 20 000 €$

Nombre de jours nécessaires pour atteindre le seuil de rentabilité en octobre.

\to \frac{458 571}{20 000} = 22,93

La date d'atteinte du seuil de rentabilité est le 23 octobre.

Remarque :

Dans l'exemple ci-avant, on suppose que les ventes sont réparties de manière linéaire sur le mois d'octobre. Si ce n'était pas le cas, pour déterminer une date plus précise, il faudrait connaître le chiffre d'affaires réalisé pour chaque jour.
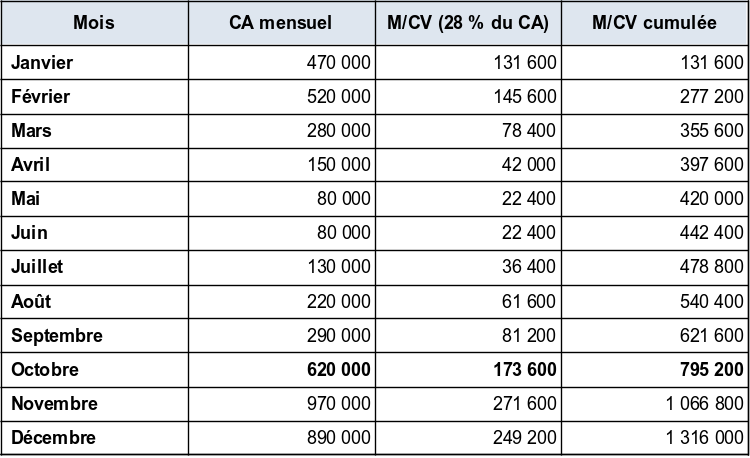
Nous aurions pu aussi passer par la M/CV cumulée → Le principe est le même que précédemment. Il suffit simplement de chercher quand la M/CV cumulée est égale au charges fixes d'exploitation.

Il vient :

On constate que la M/CV cumulée atteint le niveau de 750 000 € au cours du mois d'octobre. Mais quand en octobre ?

Résolution

M/CV/jour pour octobre \to \frac{173 60 0}{31} = 5 600

M/CV à faire pour atteindre le montant total des charges fixes → 750 000 - 621 600 = 128 400

Nombre de jours nécessaires pour atteindre le seuil de rentabilité \to \frac{128 400}{5 600} = 22,93

Vous pouvez constater que l'on retrouve exactement le même nombre de jours et donc par la même date d'atteinte du seuil de rentabilité par cette méthode.

Remarque :

Pour ce qui concerne le nombre de jours, vous pourrez bien sûr utiliser :

360 ou 365 jours pour ce qui concerne l'année,
30 ou 31 pour ce qui concerne le nombre de jours d'un mois.

Sauf avis contraire de l'énoncé, personne ne peut rien vous reprocher. N'oubliez pas en effet que nous travaillons souvent en prévisionnel et donc « on n'est pas à un jour près » ni « à une heure près » !