Étude à posteriori des charges semi-variables [Méthode des coûts variables]

Étude à posteriori des charges semi-variables

Exemple 1

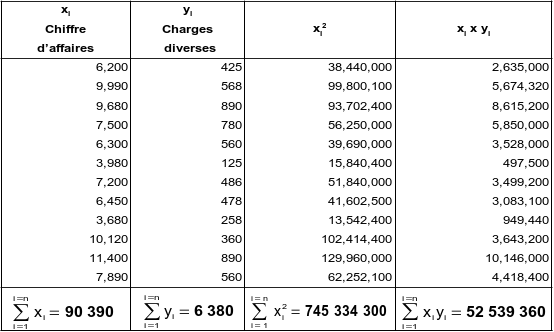
On dispose, pour l'année N de l'extrait suivant (en millions d'€) concernant des charges diverses (y_i) et du chiffre d'affaires (x_i).

On s'aperçoit d'après le tableau que les charges diverses ne sont ni fixes ni variables à 100 %.

Si elles étaient fixes à 100 %, en février par exemple, les charges diverses seraient aussi de 425.

Si elles étaient variables à 100 %, en février elles auraient dû être de : $\frac{425}{6 200} * 9 990 = 684,80$

Conséquence

Comme ce n'est pas le cas, il s'agit donc de charges semi-variables. Il faut donc séparer la partie variable de la partie fixe de ces charges semi-variables.

En admettant que, dans cet exemple, le nuage de points soit suffisamment allongé, on peut utiliser la méthode dite des moindres carrés.

Cette méthode consiste à remplacer (d'ajuster) la série par une droite de la forme : y = ax + b

Avec :

a = Charges variables unitaires
x = Activité (dans notre exemple → x correspondrait au chiffre d'affaires)
b = Charges fixes totales

Rappel :

a = \frac{Cov (xy)}{V (x)}

Covariance de (x,y) = Cov(xy) = Moyenne des produits – Produit des moyennes

Rappel :

Cov (xy) = [\frac{1}{N} \sum_{i = 1}^{i = n} x_{i} y_{i}] - (\bar{x} \bar{y}) avec N = Nombre d’observations

Variance de x = V(x) = Moyenne des carrés – Carré de la moyenne

Rappel :

V (x) = [\frac{1}{N} \sum_{i = 1}^{i = n} x_{i}^{2}] - \bar{{(x)}^{2}} avec N = Nombre d’observations

Rappel :

\begin{matrix} Moyenne de x = \bar{x} = \frac{1}{N} \sum_{i = 1}^{i = N} x_{i} \\ Moyenne de y = \bar{y} = \frac{1}{N} \sum_{i = 1}^{i = N} y_{i} \\ b = \bar{y} - a \bar{x} \end{matrix}

Remarque :

On pourrait se retrouver avec un nuage de points « alignables » par une fonction puissance ou exponentielle.

cf. cours sur gestion prévisionnelle des ventes ci-après.

Correction

Conséquence

En utilisant les formules et sachant qu'ici le nombre d'observations « N » = 12 → Il vient :

\bar{x} = \frac{1}{N} \sum_{i = 1}^{i = n} x_{i} = \frac{1}{12} * 90 390 = 7 532,50

\bar{y} = \frac{1}{N} \sum_{i = 1}^{i = n} y_{i} = \frac{1}{12} * 6 380 = 531,67

V (x) = [\frac{1}{N} \sum x_{i}^{2}] - \bar{{(x)}^{2}} = (\frac{1}{12} * 745 334 300) - 7 {532,50}^{2} = 5 372 634,4

Cov (xy) = [\frac{1}{N} \sum_{i = 1}^{i = n} x_{i} y_{i}] - (\bar{x} \bar{y}) = (\frac{1}{12} * 52 539 360) - (7 532,50  * 531,67) = 373 475,73

a = \frac{Cov (xy)}{V (x)} = \frac{373 475,73}{5 372 634,42} = 0,0695 = 6,95 %

b = \bar{y} - a \bar{x} = 531,67 - (0,0695 * 7 532,50) = 8,16

Conclusion

Avec cette méthode, la partie variable est donc égale à 6,95 % du chiffre d'affaires, et la partie fixe à 8,16 millions d'€ par mois → Soit : 8,16 * 12 = 97,92 millions d'€ pour l'exercice.

D'où la décomposition.

Remarque :

La légère différence (6 380,03 contre 6 380) vient des arrondis sur la valeur de « a ».

Exemple 2

Remarque :

Cette méthode de séparation des charges semi-variables en charges variables et en charges fixes n'est jamais utilisée dans la réalité, car elle est trop approximative ! Voilà pourquoi il est très peu probable que dans le cadre d'un examen on vous demande d'utiliser cette méthode. Nous la donnons ici simplement à titre d'information !

(1) Dans cet exemple, nous voyons que les charges fixes sont modifiées à partir d'une activité de 1 600.

→ Cela est dû probablement au fait qu'à partir de ce niveau d'activité, des investissements nouveaux sont

nécessaires et donc que des amortissements supplémentaires apparaissent !

Problème

Comment séparer la partie variable de la partie fixe des charges semi-variables ?

Solution

On va utiliser l'autre méthode dite « des points extrêmes ». Pour cela, on travaille pour un niveau d'activité compris entre 400 et 1 200.

Question

Pourquoi ne pas prendre entre 400 et 2 000 par exemple ?

Réponse

Car on doit faire cette étude pour une structure identique.

Or ici, la structure est modifiée à partir de 1 600 !

On pose : CSV = (a * x) + b

Avec x = Niveau d'activité (ici le nombre de produits fabriqués).

Nous nous trouvons donc avec un système de deux équations à deux inconnues à résoudre.

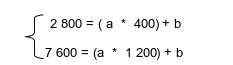
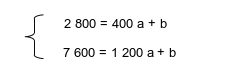
Il vient, en soustrayant par exemple la 2^ème équation du système, à la 1^ère (on supprime donc les « b »).

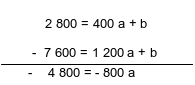
Remarque :

En faisant ainsi, on supprime la partie fixe (b) pour ne garder que la partie variable (a) !

Il vient :

→ a = $a = \frac{- 4 800}{- 800}$

→ a = 6

Pour trouver b

On reprend l'une ou l'autre des équations et on remplace « a » par la valeur que nous venons de trouver l

Il vient :

2 800 = (6 * 400) + b
Donc b = 2 800 - 2 400 = 400
ou : 7 600 = (6 * 1 200) + b → Donc b = 400

Conclusion

Charges fixes = 400 → soit b = 400

Charges variables = 6 fois l'activité → a = 6

D'où l'équation des CSV dans cet exemple → y = 6x + 400