Représentation graphique des charges (variables, fixes et semi-variables)
Les charges variables totales
Prenons les matières premières de l'exemple 2. Rappelons qu'il s'agit ici de CV à 100 %. Les charges variables sont donc représentées par une fonction de type → y = ax (x étant le niveau d'activité).
Prendre les valeurs du tableau ci-avant → Il vient :
1 200 = 400 * a → Donc
Ou
2 400 = 800 * a → Donc
Pour les matières premières, l'équation est donc la suivante → y = 3x
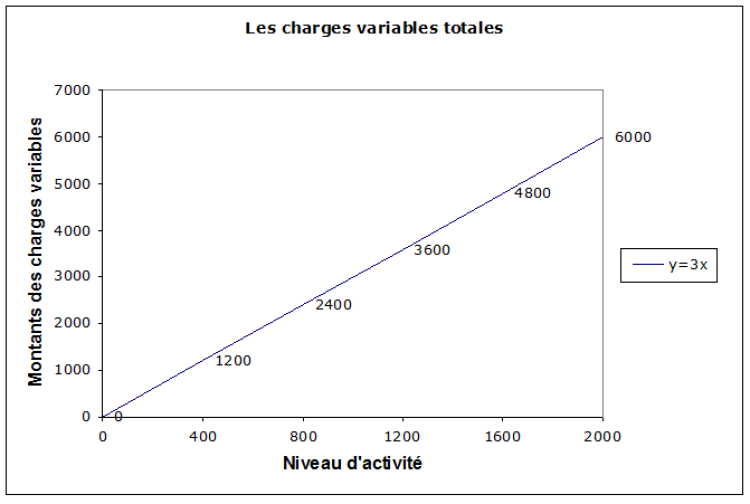
Les charges variables dépendent de l'activité. Nous voyons clairement que lorsqu'il n'y a pas d'activité, il n'y a pas non plus de consommation de matières 1ères.
Les charges variables unitaires
Gardons l'exemple des matières premières.
L'équation des CVu sera de la forme → → Après simplification, il vient → y = a
Équation des charges variables totales → y = 3 x
Équation des charges variables unitaires→ → y = 3 (après simplification)
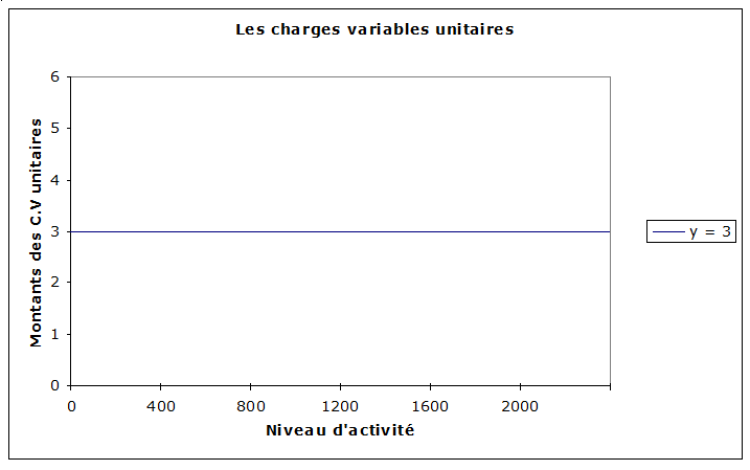
On constate que, quelle que soit l'activité, le coût unitaire de la matière 1ère reste le même.
Les charges fixes totales
Pour les charges fixes totales, nous allons prendre les amortissements de l'exemple 2. L'équation de la droite des charges fixes sera de la forme → y = b
Vous pouvez constater que le montant des amortissements reste identique pour un niveau d'activité compris entre 0 et 1 600 (plus exactement 1 599).
Pour un niveau d'activité entre 1 600 et 2 000, le montant des amortissements est de 3 500. Ceci s'appelle un effet de palier. Cet effet peut s'expliquer par la nécessité d'investir pour l'entreprise si elle souhaite augmenter son niveau d'activité. Cela peut se traduire par des achats d'immobilisations, augmentation des salaires fixes, des loyers, etc.
Dans notre exemple, pour une activité comprise entre 0 et 1 599, l'équation de la droite des amortissements sera → y = 2 000.
Pour une activité comprise entre 1 600 et 2 000, l'équation sera → y = 3 500.
On peut donc représenter graphiquement les charges fixes ainsi :
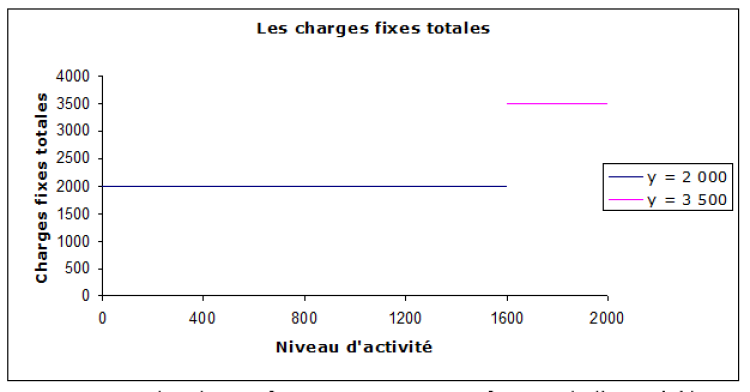
On constate que les charges fixes ne varient pas en fonction de l'activité (dans cet exemple pour un niveau d'activité compris entre 0 et 1 600).
Mais elles peuvent varier par palier, comme ici, pour un niveau d'activité supérieur à 1 600.
Les charges fixes unitaires
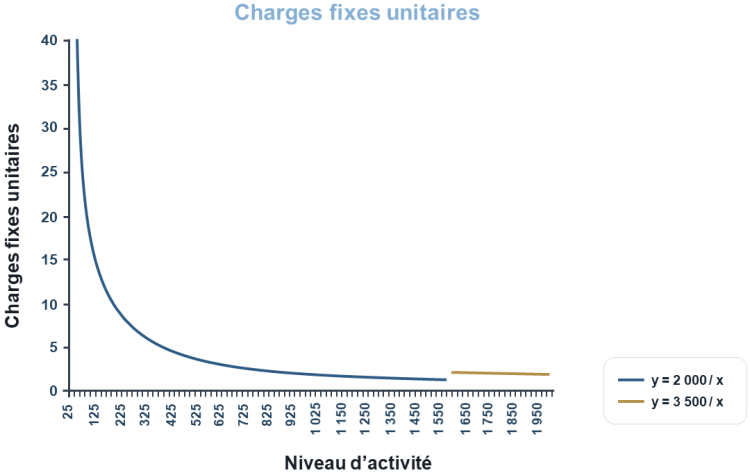
Nous reprenons toujours l'exemple des amortissements de l'exemple 2. L'équation de la droite des
charges fixes unitaires sera de la forme : y =
→ Activité comprise entre 0 et 1 599 → y =
→ Activité comprise entre 1 600 et 2 000 → y =
On peut donc les représenter graphiquement ainsi :
Les charges semi-variables totales
Toujours par rapport à l'exemple 2.
Équation des CSV → y = 6 x + 400 (pour un niveau d'activité compris entre 400 et 1 600)
Pour un niveau d'activité supérieur à 1 600, l'équation (y = 6 x + 400) n'est plus valide, car il y a un changement de structure.
Pour une représentation graphique de l'ensemble des valeurs du tableau, il aurait fallu utiliser la méthode des moindres carrés.
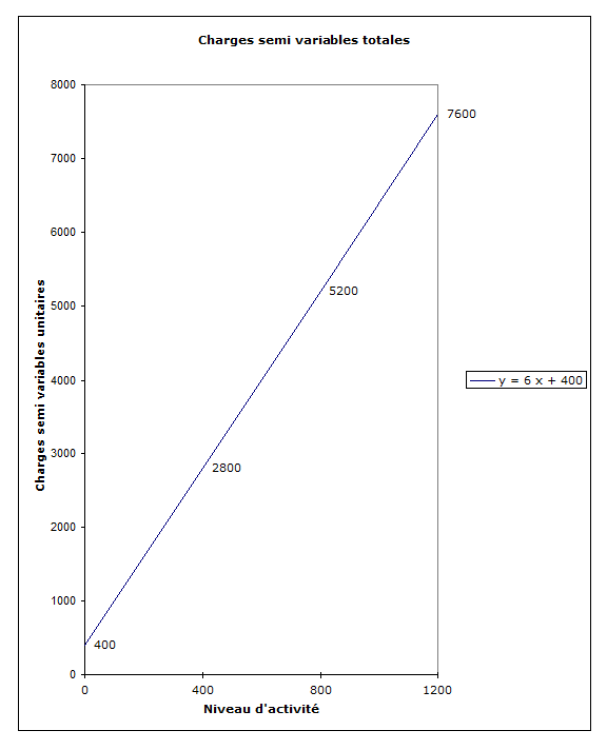
On peut constater que même si l'activité est nulle, les charges semi-variables totales comportent toujours des charges fixes.
Les charges semi-variables unitaires
Pour les charges semi-variables unitaires, l'équation de la droite est de la forme →
Dans notre exemple, l'équation est :
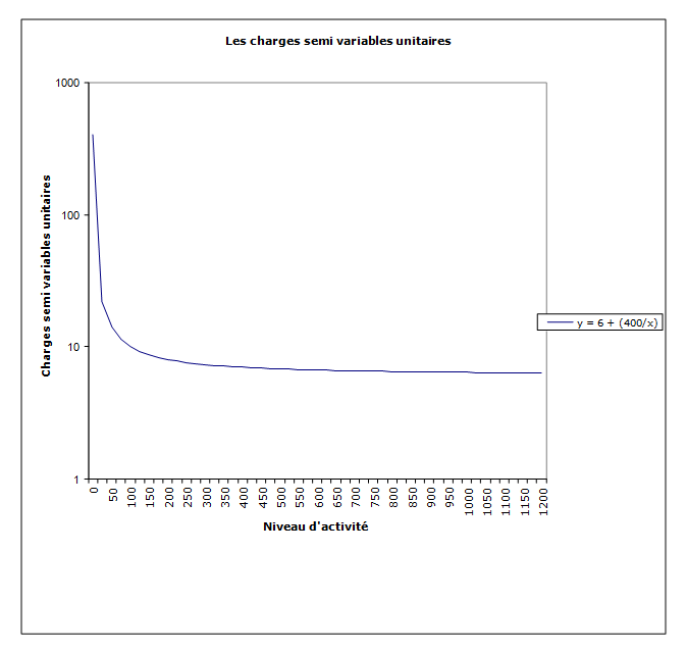
Remarque :
Pour l'axe des « y », nous avons pris une échelle logarithmique pour faciliter la représentation !
La partie variable varie en fonction de l'activité, mais la partie fixe constitue un seuil.