Élasticité-prix de la demande (ou élasticité Quantité/Prix)
Remarque : Remarque préalable
On peut calculer une élasticité simple ou une élasticité croisée.
Élasticité simple
Selon le même principe que pour le levier opérationnel (de l'incidence d'une variation du chiffre d'affaires sur le résultat), nous pouvons calculer "de l'incidence d'une variation des prix d'un article (à la hausse ou à la baisse) sur la demande du même article.
Élasticité de la demande (ED) = 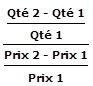 =
= 
Conséquence
L'élasticité de la demande peut être positive ou négative selon que Q2 et/ou P2 est > ou < à Q1 et P1.
Signification
Si les prix varient de x %, alors les quantités varieront de → « x » fois l'élasticité de la demande.
Si les prix baissent de 10 % par exemple, les quantités varieront de → - 0,10 * ED
Synthèse
1er cas - Baisse des prix et ED > 0
→ Les quantités varieront à la baisse.
2ème cas - Baisse des prix et ED < 0
→ Les quantités varieront à la hausse.
3ème cas - Augmentation des prix et ED > 0
→ Les quantités varieront à la hausse.
4ème cas - Augmentation des prix et ED < 0
→ Les quantités varieront à la baisse.
Élasticité croisée
Principe
L'élasticité simple permet de mesurer uniquement l'incidence de la variation des prix d'un produit sur les quantités du même produit.
L'élasticité croisée permet de mesurer l'influence de la variation du prix d'un produit sur la demande d'un autre produit. Ceci est très intéressant lorsqu'une entreprise dispose d'une gamme de produits.
Par exemple, un constructeur automobile souhaite mesurer l'influence d'une augmentation des prix de ses véhicules de début de gamme sur les ventes de ses véhicules haut de gamme.
Application
Une entreprise vend deux types de produits : A (6 500 unités) et B (4 000 unités).
Les prix de vente unitaires respectifs des produits A et B sont de 150,00 € et 200,00 €.
Le contrôleur de gestion a élaboré le tableau suivant d'élasticité croisée, en cas de hausse des prix (cf. annexe 1).
Question
Quelle serait l'incidence, sur les ventes du produit B, d'une augmentation du prix de vente unitaire du produit A de 20 % ?
Annexe 1
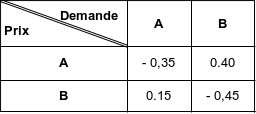
Le tableau précédent peut s'interpréter ainsi :
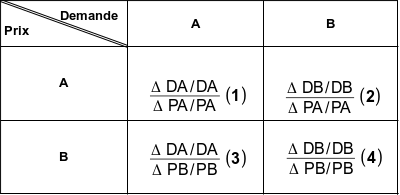
Remarque :
Le symbole Δ correspond à la lettre grecque "delta" et signifie "variation" en mathématique.
Ce que cela veut dire :
(1) → De l'incidence d'une augmentation des prix du produit A sur la demande du même produit A.
Il s'agit donc ici d'une élasticité simple !
En cas de hausse des prix du produit A de x %, la demande des produits A variera de : (x) * (- 0,35)
Autrement dit, la hausse des prix du produit A de 20 % devrait entrainer une baisse de la demande de A de :
→ + 20 % * - 0,35 = - 7 %
(2) → De l'incidence d'une augmentation des prix du produit A sur la demande du produit B.
Il s'agit donc ici d'une élasticité croisée !
En cas de hausse des prix du produit A de x %, la demande des produits B variera de : (x) * (0,40)
Autrement dit, la hausse des prix du produit A de 20 % devrait entrainer une hausse de la demande de B de :
→ + 20 % * 0,40 = 8 %
(3) → De l'incidence d'une augmentation des prix du produit B sur la demande du produit A.
Il s'agit donc ici d'une élasticité croisée !
En cas de hausse des prix du produit B de x %, la demande des produits A variera de : (x) * (0,15)
Autrement dit, la hausse des prix du produit B de 20 % devrait entrainer une hausse de la demande de A de :
→ + 20 % * 0,15 = 3 %
(4) → De l'incidence d'une augmentation des prix du produit B sur la demande du même produit B.
Il s'agit donc ici d'une élasticité simple !
En cas de hausse des prix du produit B de x %, la demande des produits B variera de : (x) * (- 0,45)
Autrement dit, la hausse des prix du produit B de 20 % devrait entrainer une baisse de la demande de B de :
→ + 20 % * - 0,45 = - 9 %
On comprend ainsi que ce tableau des élasticités croisées comprend aussi les élasticités simples [ce sont les cas (1) et (4) du tableau], dans le cas d'une augmentation des prix.
Attention :
Dans cet exemple, nous avons les élasticités croisées en cas de hausse des prix. Donc nous ne pourrions pas répondre à la question dans le cas d'une baisse des prix.
Donc si on souhaite connaître l'incidence d'une baisse des prix sur la demande de A ou de B, il faudrait que le contrôleur de gestion refasse une étude sur ce point !
Réponse à la question
Quelles sont les conséquences de cette augmentation de prix sur la demande du produit B ?
On a alors :
En clair, cela veut dire qu'une augmentation des prix de 20 % sur les produits A entraînerait une augmentation de la demande (des quantités) de 320 produits B.
Remarque :
On retrouve bien ce que nous avions évoqué précédemment.
En cas de hausse des prix du produit A de x %, la demande des produits B variera de : (x) * (0,40)
Autrement dit, la hausse des prix du produit A de 20 % devrait entraîner une hausse de la demande de B de :
→ + 20 % * 0,40 = 8 %
→ 4 000 * 8 % = + 320
On pourrait aussi trouver l'influence de cette augmentation sur les ventes du produit A (élasticité simple).
En clair, cela veut dire qu'une augmentation des prix de 20 % sur les produits A entraînerait une diminution de la demande (des quantités) de 455 produits A.
Remarque :
On retrouve bien ce que nous avions évoqué précédemment.
En cas de hausse des prix du produit A de x %, la demande des produits A variera de : (x) * (- 0,35)
Autrement dit, la hausse des prix du produit A de 20 % devrait entraîner une baisse de la demande de A de :
→ + 20 % * - 0,35 = - 7 %
→ 6 500 * - 7 % = - 455
Remarque :
Pour connaître l'influence sur le résultat de l'entreprise d'une hausse du prix des produits A, il faut bien entendu tenir compte de l'incidence de cette hausse sur les produits A et les produits B !
Dans certains énoncés, on pourrait vous demander par exemple : l'incidence d'une variation des dépenses de publicité sur le résultat de l'exercice. On applique alors exactement le même principe qu'en cas de variation des prix !
Étant donné que l'élasticité résulte de la division de « quantités » par du « chiffre d'affaires » (ou de « quantités » par des « frais de publicité »), elle n'est pas « exprimable » en %. Tout simplement, car la mesure est différente entre le numérateur et le dénominateur.