Calcul du Seuil de Rentabilité en Quantité (SRQ)

L'entreprise ne vend qu'une seule sorte de produits

Exemple

Une entreprise vend un produit P1 → Si X1 = Nombre de produits à vendre pour atteindre le seuil de rentabilité, on peut affirmer que le seuil de rentabilité en quantité sera atteint lorsque la M / CV sera égale aux charges fixes d'exploitation.

Donc, on peut écrire → (M / CV unitaire de P1 x Quantité vendue de produits X1) = CF d'exploitation

Sachant que X1 sera la seule inconnue, on peut écrire :

→ x 1 = CF d ' exploitation M / CV unitaire de P 1 bold x_{1}`=`bold {CF` d'exploitation } over bold {`M / CV `unitaire `de ` P_{1} }

Reprenons l'exemple de la section 5 – A et supposons que le prix de vente du produit est de 320,00 €.

Rappel de l'énoncé

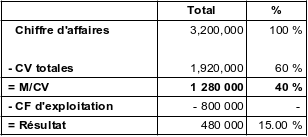
Si le PVu est de 320,00  € → L'entreprise vend donc 10 000 articles.

Donc on peut écrire :

  • M / CV unitaire en € = (320,00 * 0,40) = 128,00 €

    Ou

  • M / CV unitaire en € = 320,00 – (320,00 * 0,60) = 128,00 €

    Ou

  • M / CV unitaire en € = 1 280 000 / 10 000 = 128,00 €

Conséquence

SRQ = 800 000 / 128,00 = 6 250 unités

Donc, pour atteindre son SRQ, l'entreprise devra vendre 6 250 produits.

Vérification

Si SRQ = 6 250 → Alors seuil de rentabilité en € → 6 250 * 320,00 = 2 000 000 €.

On retrouve bien le même seuil de rentabilité en € que précédemment.

Remarque

Une autre approche est possible → SRQ =  SR en € PVu `bold {SR `en ` €} over bold {`PVu } → SRQ =  2 000 000 320 = 6 250 ( produits ) ` {2`000`000} over {`320 }` =`6`250`(produits)

NB : Des solutions graphiques sont possibles pour trouver le seuil de rentabilité en quantité.

1ère solution pour trouver le SRQ par le graphique

  • En ordonnée : y = Équation du résultat = (M / CV unitaire *  x) – CF.

  • En abscisse : x = Quantités.

→ À l'intersection de « y » et de « x », on a : résultat = 0 → Le SR en quantité.

→ Dans notre exemple : y = (128,00 * x) – 800 000

Attention

Dans l'hypothèse d'un SRQ qui n'est pas un chiffre entier, il faut arrondir à l'unité supérieure → Le seuil de rentabilité sera alors atteint avec certitude.

Représentation graphique du SR en quantités

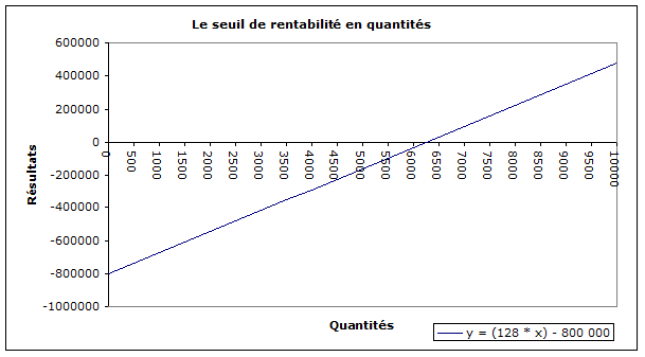
Le SRQ est atteint lorsque la droite du résultat coupe l'axe des abscisses.

À la lecture du graphique ci-dessus, on trouve le SRQ égal à 6 250 produits.

Toujours à partir du même exemple :

A la lecture du point d'intersection des deux droites, on trouve le SRQ.

2ème solution pour trouver le SRQ par le graphique

  • En ordonnée :

    • y1 = Équation de la M / CV totale → y1 = (M / CV unitaire * x)

    • y2 = CF

  • En abscisse : x = Quantités

Toujours à partir du même exemple :

  • y1 = 128,00 * x

  • y2 = 800 000

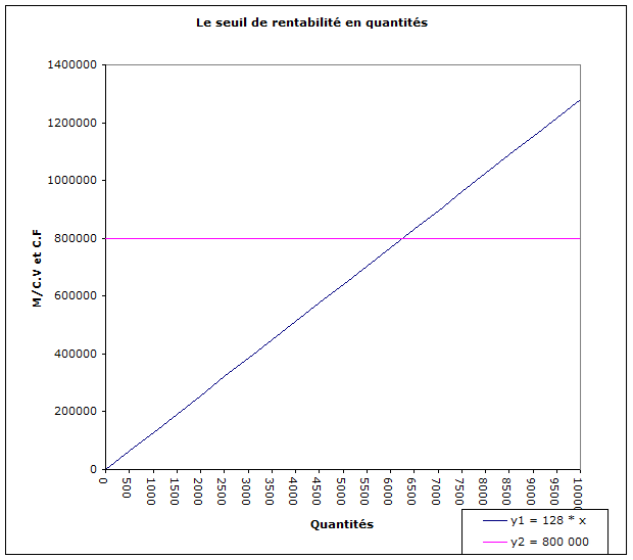
À la lecture du point d'intersection des deux droites, on trouve le SRQ.

Ici on retrouve bien le nombre de 6 250 produits.

L'entreprise vend plusieurs sortes de produits

1er exemple

Une entreprise vend trois sortes de produits :

  • A → 20 000 articles à 3,00 € l'unité

  • B → 30 000 articles à 3,50 € l'unité

  • C → 50 000 articles à 2,00 € l'unité

La M/CV unitaire (en €) de chaque type de produit est :

  • A →  1,20 €

  • B → 1,05 €

  • C → 0,40 €

Les charges fixes d'exploitation sont de 39 000,00 €.

Question

Combien doit-on vendre de produits de chaque type pour atteindre le seuil de rentabilité ?

Correction

Il existe deux méthodes pour résoudre ce type de problème. Toutefois bien comprendre qu'il faut respecter le principe suivant : le seuil de rentabilité pour un produit doit respecter la même proportion (par rapport au seuil de rentabilité total) que pour le chiffre d'affaires généré par ce produit (par rapport au chiffre d'affaires total) !

1ère méthode de résolution

M/CV totale = (20 000 * 1,20) + (30 000 * 1,05) + (50 000  * 0,40) = 75 500,00 €

CF totales = 39 000,00 €

CA total = (20 000 * 3,00) + (30 000 * 3,50) + (50 000 * 2,00) = 60 000 + 105 000 + 100 000 = 265 000,00

Donc, SR total en € = (265 000,00 * 39 000,00) / 75 500,00 = 136 887,42 €

Donc, SR en € par produit :

  • Pour A

    → 136 887,42 * (60 000,00 / 265 000,00) = 30 993,38 €

    Sachant que 60 000,00 = Le CA total généré par les produits A

  • Pour B

    → 136 887,42 * (105 000,00 / 265 000,00) = 54 238,41 €

  • Pour C

    → 136 887,42 * (100 000,00 / 265 000,00) = 51 655,63 €

Donc le SRQ par produit est le suivant :

  • Pour A

    → 30 993,38 / 3,00 = 10 331,13 → Arrondi à 10 332 unités

  • Pour B

    → 54 238,41 / 3,50 = 15 496,69 → Arrondi à 15 497 unités

  • Pour C

    → 51 655,63 / 2,00 = 25 827,81 → Arrondi à 25 828 unités

2ème méthode de résolution

Si on appelle, XA, XB, XC le SR en quantité de chaque produit, on peut écrire :

→ (M / CVu de A * XA) + (M / CVu de B * XB) + (M / CVu de C * XC) = CF totales

Nous respectons bien la définition du SR → Au SR, la M/CV doit être égale aux charges fixes totales.

Il vient :

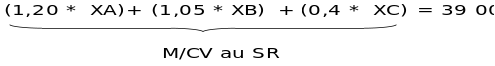
On se retrouve avec une équation à plusieurs inconnues ! La seule méthode pour la résoudre c'est d'utiliser des équivalents pour chaque produit.

Par exemple, prenons B comme équivalent en quantités → Il vient :

  • A =  2 / 3 * B → 2 / 3 = (20 000 / 30 000)

  • C = 1,67 * B → 1,67 = (50 000 / 30 000)

En reprenant l'équation ci-dessus, on obtient :

→ [1,20 * (2 / 3 B)] + (1,05 * B) + (0,40 * 1,67 B) = 39 000,00

→ 0,80 B + 1,05 B + 0,6667 B = 39 000,000

→ 2,51667 B = 39 000,00

→ B = 15 496,67

On retrouve bien le même SRQ pour le produit B qu'avec la première méthode.

→ Pour le produit A → 15 496,67 * 2 / 3 = 10 331,12

→ Pour le produit C → 15 496,67 * 1,67 = 25 827,79

Nous retrouvons bien les mêmes SRQ qu'avec la première méthode.

Pour obtenir le SR en €, il suffit de multiplier les quantités par le prix de vente unitaire de chaque produit.

→ Pour le produit A → 10 331,12 * 3 = 30 993,36 (SR en €)

→ Pour le produit B → 15 496,67 * 3,50 = 54 238,34

→ Pour le produit C → 25 827,79 * 2 = 51 655,58

2ème exemple

Une entreprise vend deux produits P1 et P2.

  • M/CV unitaire de P1 = 75,00 €

  • Prix vente unitaire de P1 = 230,00 €

  • M/CV unitaire de P2 = 90,00 €

  • Prix de vente unitaire de P2 = 320,00 €

  • Charges fixes d'exploitation = 250 000,00 €

Question

Calculer le seuil de rentabilité en quantité et le seuil de rentabilité en € par type de produits, sachant que l'on vend deux fois plus de P1 que de P2.

Correction de l'exemple 2

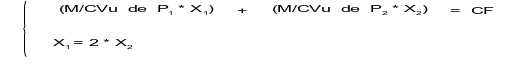
Donc il vient, en remplaçant dans la 1ère équation X1 par sa valeur :

→ (75,00 * 2 * X2) + (90,00 * X2) = 250 000,00

→ (150,00 * X2) + (90,00 * X2) = 250 000,00

→ 240 * X2 = 250 000,00 → X2 = 1 041,67

→ X1 = 1 041,67 * 2 = 2 083,33

Solution

  • SRQ de P1 = 2 084 produits

  • SRQ de P2 = 1 042 produits

  • SR en € de P1 = 2 084 * 230,00 = 479 320,00 €

  • SR en € de P2 = 1 042 * 320,00 = 333 440,00 €

3ème exemple

  • M/CV unitaire de P1 = 75,00 €

  • M/CV unitaire de P2 = 90,00 €

  • Prix de vente unitaire de P1 = 145,00 €

  • Prix de vente unitaire de P2 = 240,00 €

  • Charges fixes d'exploitation = 250 000,00 €

Question

Calculer le seuil de rentabilité en quantité et le seuil de rentabilité en € par type de produits, sachant que le chiffre d'affaires réalisé par P1 est supérieur de 10 % à celui réalisé par P2.

Correction de l'exemple 3

Si on appelle X1, X2 le SR en quantité de chaque produit, on peut écrire :

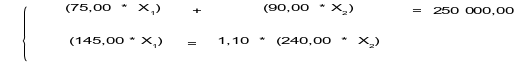
Donc à partir de la 2ème équation ; on peut écrire :

→ (145,00 X1) = 264,00 * X2  → X1 = → X1 = 1,82 X2

En remplaçant dans la 1ère équation X1 par la valeur que nous venons de trouver, il vient :

→ (75 * 1,82 X2) + (90,00 * X2) = 250 000,00

→ 226,50 X2 = 250 000,00

X2 = 1 103,75 → 1 104 unités

→ Ayant trouvé X2, on peut maintenant trouver X1 :

→ (145,00 * X1) =1,10 * (240,00 * 1 104) 

→ (145,00 * X1) = 291 456

→ X1 = 2 010,04 → 2 011 unités

Vérification

La M/CV doit couvrir les charges fixes pour atteindre le SR.

(75 * 2 010,04) + (90 * 1 103,75) = 250 090,50

  • SR en € pour P1 → 2 011 * 145,00 = 291 595,00 €

  • SR en € pour P2 → 1 104 * 240,00 = 264 960,00 €